1、取参数t,θ,r,a,b,并设定范围;
2、输入圆上一点A=(a+rcosθ,b+rsinθ;
3、输入圆的方程(x-a)²+(y-b)²=r²;
4、输入圆的切线的参数方程(a+r cos(θ)-sin(θ) t,b+r sin(θ)+cos(θ) t),并显示轨迹。
圆的切线参数方程
2023-06-01 17:17:05
模板评价:
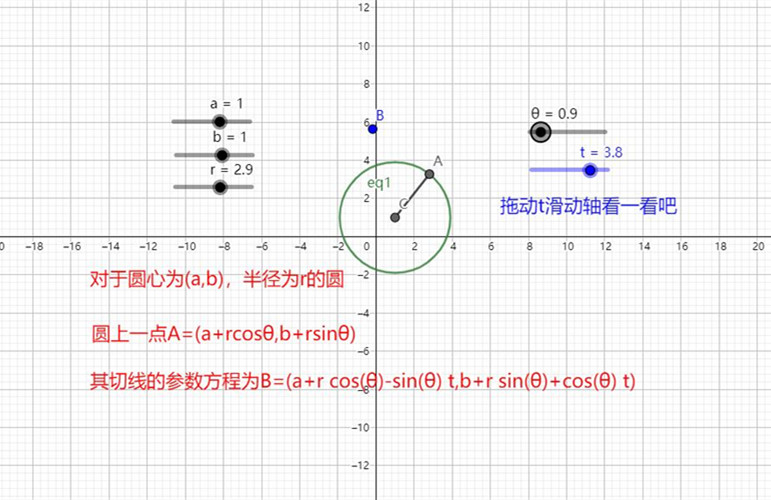
这是一份高中数学圆的切线参数方程图像模板文件,通过拖动改变θ的位置移动圆的切线位置,拖动滑动条t的值,观察圆的切线轨迹。MathTool可以帮助用户轻松制作圆的切线参数方程知识点的教学设计,提升课堂交互演示效果。
100%
模板构建过程
知识点详情描述
方程(x-a)²+(y-b)²=r²为以点O(a,b)为圆心,半径为r的圆,对于圆上一点A(a+rcosθ,b+rsinθ),其切线方程为:cosθ(x-a)+sinθ(y-b)=r。
其证明过程如下:
设切线上一点P=(x,y),向量OA=(rcosθ,rsinθ),向量AP=(x-a-rcosθ,y-b-rsinθ)
由圆的几何知识可知向量OA·向量AP=0,即rcosθ(x-a-rcosθ)+rsinθ(y-b-rsinθ)=0
其证明过程如下:
设切线上一点P=(x,y),向量OA=(rcosθ,rsinθ),向量AP=(x-a-rcosθ,y-b-rsinθ)
由圆的几何知识可知向量OA·向量AP=0,即rcosθ(x-a-rcosθ)+rsinθ(y-b-rsinθ)=0









